期權定價模型有很多,但是投資者比較常用的就屬于b-s-m定價模型以及b-s模型,本篇文章我們主要說說b-s-m定價模型和b-s模型的區別都有哪些?
b-s-m定價模型和b-s模型的區別
b-s-m定價模型
1、B-S-M模型的假設(初始)
①在期權壽命期內,買方期權標的股票不發放股利,也不做其他分配;
②股票或期權的買賣沒有交易成本;
③短期的無風險利率是已知的,并且在期權壽命期內保持不變;
④任何證券購買者能以短期的無風險利率借得任何數量的資金;
⑤允許賣空,賣空者將立即得到所賣空股票當天價格的資金;
⑥看漲期權只能在到期日執行;
⑦所有證券交易都是連續發生的,股票價格隨機游走。
2、B-S-M期權估價模型 ?
僅適用于歐式期權;假設不發股利,如果發股利,模型需要調整。
C:看漲期權的價格;
P:看跌期權的價格;
S0:基礎資產在初始0時刻的價格;
K:期權的執行價格;
r:連續復利無風險利率;
σ:基礎資產價格百分比(收益率)的年化波動率;
T:期權合約的期限(年);
N(*):累積標準正態分布的概率密度。
3、支付紅利的B-S-M模型
4、期權變量與相關價格的關系
隨著基礎資產股票價格的上升,看漲期權的價格會增大,看跌期權的價格會減少。此外,基礎資產價格的變化與期權價格的變化之間存在非線性關系。
5、期權價格與執行價格的關系
隨著期權執行價格的上升,看漲期權的價格會減少,看跌期權的價格會增加。此外,基礎資產價格的變化與期權價格的變化之間存在非線性關系。?
6、期權價格與無風險利率的關系 ?
? ?
?無風險利率增加時,歐式看漲期權的價格上升,看跌期權的價格下跌。
7、期權價格與紅利的關系?
隨著紅利現值的上升,看漲期權的價格會減少,看跌期權的價格會增加。此外,基礎資產價格的變化與期權價格的變化之間存在非線性關系。
期權價格與到期期限的關系
無論是歐式看漲期權或是歐式看跌期權,期權價格通常是期權期限的遞增函數,但是當期限很短時,這一結論可能不成立。
需要注意的是,美式看漲或看跌期權,由于可以提前行權,因而到期期限越長,期權的價格就越大。
8、期權價格與股價波動率的關系
隨著股價的波動率增加,歐式看漲或看跌期權的價格都會增加,但是波動率的變化與期權價格的變化依然是一種非線性關系。
b-s模型
B-S模型的假設條件:?
(1)無風險利率r是已知的,為一個常數,不隨時間的變化而改變
(2〉標的證券為股票,正股價格s的變化符合隨機漫步,但這種隨機漫步能夠使股票的回報率成對數正態分布。
(3)標的股票不分紅
(4)期權為歐式期權,即到期日才能行權
(5)整個交易過程中,不存在交易費用,沒有印花稅
(6)對賣空沒有如保證金等任何限制,投資者可自由使用賣空所得資金
計算方法:
C——看漲期權的當前價值;
P——看跌期權的當前價值;?
X——期權的執行價格;?
S——標的股票的當前價格;
t——期權到期日前的時間(年);?
r——連續復利的年度無風險利率;?
N(d)——標準正態分布中離差小于d的概率;?
e——自然對數的底數,約等于2.7183
計算方法參考:
來源:十三財經

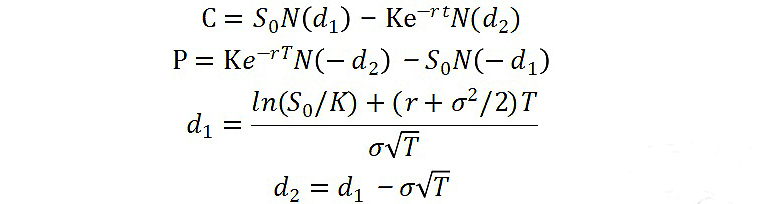
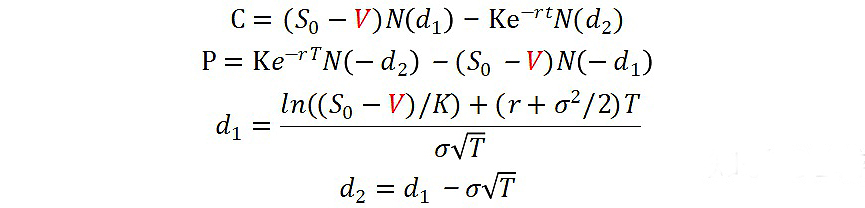



評論前必須登錄!
立即登錄 注冊